As we approach the end of the year it is always good to reflect on the year gone by, and on our place in the universe, miserable as that place frequently is.
An archaic, but still useful, aid for visualization is the Kepner-Tregoe Matrix. So, I have taken time to reflect on the travails of the search for 9M-MRO, and summarize what we know and can reasonably postulate with the Kepner-Tregoe Matrix below.
COLOR CODE
Red - Not at all Compatible
Yellow - Weakly Compatible
Green - Strongly Compatible
Friday, December 30, 2016
Saturday, December 24, 2016
Is Something Wrong with this Picture (The Search for 9M-MRO) ??
From
Forward I page v of
"Bayesian Methods in the Search for MH370:
Uncertainty
is all pervasive—whether it relates to everyday personal choices
and actions, or as background to business and policy decisions, or
economic and climate predictions. In recent times, few things have
attracted as much attention as the uncertainty surrounding the final
whereabouts of MH370.
Yes,
indeed.
A
cadre (and a large cadre at that) of very qualified people have
tossed their hat in the uncertainty reduction ring - the SSWG, the
DSTG, CSIRO, to name a few. I will refer to this group as the SSI,
Search Strategy Insiders. The SSI has representatives from Boeing,
Inmarsat, and Thales. Who can claim to know more about the
performance characteristics of a 777 aircraft than Boeing? Who can
claim to know more about the Inmarsat system than Inmarsat? Who can
claim to know more about how the AES functions than Thales?
Additionally
the SSI has access to 20 previous flights of 9M-MRO. The data from
these 20 previous flights includes the ACARS data, so the SSI knows
exactly where the aircraft was located, the ground track of the
aircraft, and the fuel consumption relative to these 20 previous
flights. Data of this type has never been made available to anyone
but the SSI.
From
page 27 of "Bayesian Methods..." referring to the BTO
calibration/validation:
The
data used to construct the histogram and the empirical parameters
were obtained from logs of the 20 flights of 9M-MRO prior to the
accident flight.
From
page 30 of "Bayesian Methods..." referring to the
collection of BFO statistics:
Empirical
statistics of the residual measurement noise wBFOk
were determined using the previous 20 flights of 9M-MRO. Data points
corresponding to when the aircraft was climbing or descending were
excluded.
The
SSI also has access to the radar data, not simply graphics, which has
never been put in the public domain. It is fair to say that the SSI
has a great deal of information that allows them to test and to
refine their modeling. The rest of us have nothing but the Inmarsat
logs from the accident flight, so there is no way to validate our own
modeling. Still, the terminal locations derived by the SSI are
consistent with the terminal locations derived by the rest of us.
There is obviously no magic here.
So,
what is the take-away? My early conclusion is that the ensemble of
data associated with the accident flight is not sufficient to
determine a terminus, and so would conclude any other person
reasonably skilled in the background analytics. The data can only
broadly constrain the possible terminal locations. It cannot
constrain terminal locations sufficiently well to have a high degree
of confidence in the results of an under water search conducted in a
relatively small area.
The only things wrong are our expectations.
The only things wrong are our expectations.
Tuesday, December 20, 2016
Vendee Globe Predictions
In progress as I type this is a solo around the world sailboat race originating and ending in France. You can read all about it at the link below.
ranking-and-race-data
The race is quite interesting in its own right. Fewer people have participated in it over the years than have climbed Mount Everest. It truly is daunting.
It also serves as an interesting test bed for statistical prediction.
Using the daily progress to date and a Monte Carlo simulation (500 trials). The winning time is predicted to be in the range of 65 to 69 days (95% probability). Previous record time was the last time the race was held in 2013, and was 78 days. The predicted improvement is largely attributed to boats with foils being used for the first time.
Another interesting statistical question is how many sailors will still be in the race when the winner arrives in France. This value was estimated using Poisson statistics, and is shown below. When the analysis below was run there were 10 abandons(8 declared officially and 2 more likely but undeclared). So the number of abandons at the end of the race (when winner crosses the line) should be in the range of 12 to 17 with high confidence, and with a predicted most likely value of 14/15. Since 29 boats started the race, that would imply 15/14 boats still heading to France.
The motive for posting this information is similar to the IG motive for sticking pins in a map. It serves the purpose of going on record with your analytics so they can be tested against reality in the future.
So, we shall see.
Update 23 December:
So, as the leader rounds Cape Horn it becomes obvious that the weather pattern heading North in the Atlantic is far different than the weather pattern that prevailed in the traverse from Good Hope to Cape Horn. As a consequence, the Monte Carlo simulation is likely to be too optimistic relative to predicting the finishing time. Hey, you can only do so much. The abandon model is not affected.
Update 24 December:
Leader's daily progress from start. Linear fit has been excellent, but it is unlikely to continue sailing North in the Atlantic.
Histogram of daily distance (48 days total) recorded by the leader. I have no explanation for the obvious bimodal distribution.
Update 27 December
So, I have a conjecture for the bimodal distribution above. The conjecture being that there is a threshold speed for the foil boats that produces two normal speed distributions - one above and one below the speed where the foils add lift. Of course, this will need to be checked by downloading the data for a non-foil boat such as Rich Wilson's. Just FYI the transition speed (if there is one) based on the bimodal distribution above is around 14.5 knots.
Update 28 December
So, I harvested the Rich Wilson data and plotted it on the same histogram using the same range bins as the above data plot.
The Wilson data does not exhibit the marked bimodal characteristic of the leading foil boat. I am not prepared to draw a broad conclusion here. Obviously more work needs to be done using data from other boats.
Update 2 January
Harvested the daily distance cover by Elies (non-foil boat) and plotted histogram (below).
Today is my birthday!
Should have done this above, but neglected to do so (old and lazy). Check Weibull fit against the 11 failures to date. The failures to date are plotted as red dots in the Weibull CDF. As can be seen, the actual failures are running ahead of the Weibull prediction. However, there has not been a failure for some time now, so the actual data should revert to the Weibull prediction CDF as more boats fail.
While here I am here I may as well post the latest first boat ETA Monte Carlo. Used finer granularity and 10,000 trials. The French prediction of January 19 is day 74. The French prediction is looking pretty good right now, although it could easily spill over into January 20. Of course, I am sticking with the original Monte Carlo prediction of 73 days for statistical critique purposes. Perhaps we will have a "regression to the mean", and I will be able to pontificate on that.
Also below is the leader current daily distance. Obviously had the daily distance kept pace with the trend between Good Hope and The Horn there would have been partying going on in France a day or so ago.
The first data point for statistical confirmation is "in the books". Rich Wilson rounded Cape Horn on January 16 at ~0300UTC which, according to my math, is race elapsed time of 71.63 hours. From Vendee website below:

The Monte Carlo prediction for the rounding is reproduced below.
I would categorize the agreement as good.
More data on boat speed (histograms for 71 days) is shown below for Banque and CoQ, currently running 1st and 3rd respectively. The data is clearly not Gaussian, but shows evidence of "binning" with a bin separation near 10 knots and 15 knots. My speculation is the 10 knot null is due to a "hull speed" effect. The hull speed of a 60' boat is ~10 knots, 1.34*SQRT(60) ~ 10. The bin separation near 15 knots is due to the foils which are said to become effective around that speed.
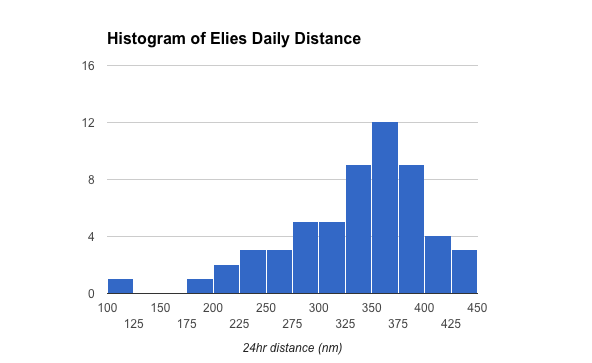
The tri-modality for CoQ is not as pronounced as Banque, but it is clearly there. The non-foil boats exhibit a histogram which is more nearly Gaussian, although there is a hint of a hull effect in the Elies data, a non foil boat, also shown below.
Update 19 January
The winning boat arrived in port today with an elapsed time of 74:03:36 , 74.15 days. This value is shown in red below on the Monte Carlo histogram derived earlier.
ranking-and-race-data
The race is quite interesting in its own right. Fewer people have participated in it over the years than have climbed Mount Everest. It truly is daunting.
It also serves as an interesting test bed for statistical prediction.
Using the daily progress to date and a Monte Carlo simulation (500 trials). The winning time is predicted to be in the range of 65 to 69 days (95% probability). Previous record time was the last time the race was held in 2013, and was 78 days. The predicted improvement is largely attributed to boats with foils being used for the first time.
Another interesting statistical question is how many sailors will still be in the race when the winner arrives in France. This value was estimated using Poisson statistics, and is shown below. When the analysis below was run there were 10 abandons(8 declared officially and 2 more likely but undeclared). So the number of abandons at the end of the race (when winner crosses the line) should be in the range of 12 to 17 with high confidence, and with a predicted most likely value of 14/15. Since 29 boats started the race, that would imply 15/14 boats still heading to France.
The motive for posting this information is similar to the IG motive for sticking pins in a map. It serves the purpose of going on record with your analytics so they can be tested against reality in the future.
So, we shall see.
Update 23 December:
So, as the leader rounds Cape Horn it becomes obvious that the weather pattern heading North in the Atlantic is far different than the weather pattern that prevailed in the traverse from Good Hope to Cape Horn. As a consequence, the Monte Carlo simulation is likely to be too optimistic relative to predicting the finishing time. Hey, you can only do so much. The abandon model is not affected.
Update 24 December:
Leader's daily progress from start. Linear fit has been excellent, but it is unlikely to continue sailing North in the Atlantic.
Histogram of daily distance (48 days total) recorded by the leader. I have no explanation for the obvious bimodal distribution.
Update 27 December
So, I have a conjecture for the bimodal distribution above. The conjecture being that there is a threshold speed for the foil boats that produces two normal speed distributions - one above and one below the speed where the foils add lift. Of course, this will need to be checked by downloading the data for a non-foil boat such as Rich Wilson's. Just FYI the transition speed (if there is one) based on the bimodal distribution above is around 14.5 knots.
Update 28 December
So, I harvested the Rich Wilson data and plotted it on the same histogram using the same range bins as the above data plot.
The Wilson data does not exhibit the marked bimodal characteristic of the leading foil boat. I am not prepared to draw a broad conclusion here. Obviously more work needs to be done using data from other boats.
Update 2 January
Harvested the daily distance cover by Elies (non-foil boat) and plotted histogram (below).
There is not a hint of a bimodal distribution. This result tells me there is a threshold effect going on with the foil boats i.e. slower below a certain threshold, and a non-linear increase in speed above a certain threshold. Probably this non-linearity is to be expected? Foils create more drag below threshold, and provide a lift (step function reduction in drag) above a certain threshold. As stated above this threshold speed is in the neighborhood of 14.5 knots.
Update 3 January
The weather in the South Pacific has been horrible. Despite that Wilson put in an impressive 24hr run.
South Atlantic continues to slow the pace of the lead boats as the trend line below clearly shows.
Updated Wilson/Leader histogram. Wilson's data has regressed to essentially Gaussian form.
Winning time propagator has advanced to 69 days. My guess is that this advance will continue or perhaps even accelerate as the leaders hit the doldrums. MOQ is definitely closing in, and may well become a factor.
Update 4 January
Continuing to look at the daily distance distribution, I harvested the daily totals of CoQ, another foil boat, and plotted the histogram below.
Leader histogram reproduced again below for comparison.
CoQ does not exhibit a strong bimodal distribution. This data would seem to contradict the notion that there is a threshold effect with respect to the foil boats. While CoQ has achieved a higher daily distance than the leader, it is interesting to note that the number of days in which 450nm or more was achieved is 12 for the leader versus 4 for CoQ.
Update 6 January
So, being someone who sings the US National Anthem, I was curious to see what Monte Carlo had to say about Rich Wilson's finishing (Rich has better than a 66% chance of finishing). Histogram below.
Of course, weather is a huge factor as we are seeing relative to the obvious slow down in the lead boat relative to the trend line established earlier in the race.
Update 7 January
So, the French have thrown their hat into the ETA prediction ring. The linked article below appeared in the last day.
Of course, the later the prediction, the more information you have. There is also less uncertainty since there is less time remaining. While I stand my original estimate made some three weeks ago, if I were to update the Monte Carlo run with the following priors the result would be as shown below.
1> Leader was rounding Cape Horn on December 23 (day 48)
2> Leader currently has ~3000nm remaining distance to travel
3> Draw Monte Carlo samples from post Cape Horn data set (days 48-62)
The result above is in good agreement with the recent French prediction.
Update 10 January
For Rich Wilson followers a prediction below for when he is likely to round Cape Horn. All 500 Monte Carlo trials fell into bin days 71,72, and 73 with day 72 dominant with a ~70% probability.
update 12 January
So earlier I used Poisson statistics to compute how many boats would abandon by the time the lead boat finished. The question was posed in this way for my convenience. A much more difficult, and interesting, question to answer is how many boats will finish the race. To answer this question requires Weibull statistics which are much more difficult and tedious than Poisson (which is why I do not generally pose questions in that way).
The array below is the ordered percentage complete of the boats that have abandoned the race so far.
data = np.array([4,16,29,29,30,36,45,49,54,55,56]) #11 boats have officially abandoned the race
Additionally there are 18 boats still in the race. The array data above must be "censored". Censoring is a term mathematicians use for the need to adjust the failure rank by the number of "units" that have not failed at the time the calculation was performed.
When the array data (properly censored) is plotted on the standard Weibull ln-ln plot the result is as shown below. The extent to which these points fall on a straight line on a ln-ln plot is a measure of the appropriateness of the Weibull statistic.
Using linear regression a best fit straight line is fitted to the above data as shown below.
While not perfect, the straight line fit is far from horrible. The Weibull statistic should work pretty well. Extracting the slope and intercept of the linear regression yields the "shape" and "scale" factors of the Weibull distribution which allows the Weibull CDF (cumulative distribution function) to be plotted below.
The CDF shows that at 100% complete the percent abandoning is very close to 50%. So Weibull statistics predict that half the starting field (~15 boats) should be able to finish.
P.S. Earlier I mentioned that Wilson had better than a 66% chance of finishing. I got that number in a simplistic fashion. While true, the reality is that Wilson has a better than 80% chance of finishing now that a proper number for the total finishers has been computed.
(1) references from the weibull.nl website and also from this example of doing Weibull analysis using Excel.
(2) reference code from pybokeh at wakari.io Weibull Analysis Notebook
Update 14 January
Should have done this above, but neglected to do so (old and lazy). Check Weibull fit against the 11 failures to date. The failures to date are plotted as red dots in the Weibull CDF. As can be seen, the actual failures are running ahead of the Weibull prediction. However, there has not been a failure for some time now, so the actual data should revert to the Weibull prediction CDF as more boats fail.
While here I am here I may as well post the latest first boat ETA Monte Carlo. Used finer granularity and 10,000 trials. The French prediction of January 19 is day 74. The French prediction is looking pretty good right now, although it could easily spill over into January 20. Of course, I am sticking with the original Monte Carlo prediction of 73 days for statistical critique purposes. Perhaps we will have a "regression to the mean", and I will be able to pontificate on that.
Also below is the leader current daily distance. Obviously had the daily distance kept pace with the trend between Good Hope and The Horn there would have been partying going on in France a day or so ago.
Update 17 January
The first data point for statistical confirmation is "in the books". Rich Wilson rounded Cape Horn on January 16 at ~0300UTC which, according to my math, is race elapsed time of 71.63 hours. From Vendee website below:

The Monte Carlo prediction for the rounding is reproduced below.
More data on boat speed (histograms for 71 days) is shown below for Banque and CoQ, currently running 1st and 3rd respectively. The data is clearly not Gaussian, but shows evidence of "binning" with a bin separation near 10 knots and 15 knots. My speculation is the 10 knot null is due to a "hull speed" effect. The hull speed of a 60' boat is ~10 knots, 1.34*SQRT(60) ~ 10. The bin separation near 15 knots is due to the foils which are said to become effective around that speed.
The tri-modality for CoQ is not as pronounced as Banque, but it is clearly there. The non-foil boats exhibit a histogram which is more nearly Gaussian, although there is a hint of a hull effect in the Elies data, a non foil boat, also shown below.
Update 19 January
The winning boat arrived in port today with an elapsed time of 74:03:36 , 74.15 days. This value is shown in red below on the Monte Carlo histogram derived earlier.
I am quite satisfied with this result, and will have more to say about the method and my impressions in a later post. For the moment it is safe to say that three factors (all weather related) place fundamental constraints on what accuracy might be achieved:
1> Distance traveled each day which, as I understand it, is the great circle distance covered in a 24 hour period. What is really of interest is the distance "made good".
2> A related issue is the total distance traveled. My simulation used a value of 25,260 nm whereas at the end of the race the leader had traveled 27,445 nm.
Without further study I am not prepared to say whether the above two effects act counter to each other or reinforce each other. My suspicion is the former since the accuracy turned out very well.
3> The weather itself is not predictable, and its effect is not equivalent to white noise that averages out.
Tuesday, December 13, 2016
Debris Statistics
What can we say based on the confirmed and likely MH370 debris found so far? By my count there have been eight pieces of debris in these categories (three confirmed and five likely) found in the last sixteen months (since the right flaperon in July, 2015).
It is well known that the Poisson distribution is appropriate for calculating event probabilities - from Wiki below:
Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time and/or space if these events occur with a known average rate and independently of the time since the last event.
In the case of MH370 debris finds the lambda value, based on eight pieces over 16 months, is calculated to be 0.5 (starting with the right flaperon in July 2015)
So the trivial calculation above yields the following:
P(0) ~ 0.60 // probability of no confirmed or likely pieces being found in any given month
P(1) ~ 0.30 // probability of one confirmed or likely piece being found in any given month
P(>1) ~ 0.10 // probability of two or more confirmed or likely pieces being found in any given month
Of course, the rate of debris finds is highly dependent on the level of search activity. The above numbers assume it will be the same going forward as it has been in the past i.e. not very much.
It is well known that the Poisson distribution is appropriate for calculating event probabilities - from Wiki below:
Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time and/or space if these events occur with a known average rate and independently of the time since the last event.
In the case of MH370 debris finds the lambda value, based on eight pieces over 16 months, is calculated to be 0.5 (starting with the right flaperon in July 2015)
So the trivial calculation above yields the following:
P(0) ~ 0.60 // probability of no confirmed or likely pieces being found in any given month
P(1) ~ 0.30 // probability of one confirmed or likely piece being found in any given month
P(>1) ~ 0.10 // probability of two or more confirmed or likely pieces being found in any given month
Of course, the rate of debris finds is highly dependent on the level of search activity. The above numbers assume it will be the same going forward as it has been in the past i.e. not very much.
Debris Planting - Nuances and Issues
A fair amount of play has recently been given to the possibility that the debris associated with MH370 has been planted for some (as yet not well-articulated) reason. I see several issues with that conjecture:
- If the debris was planted the implication is that there is no real debris. Since virtually every crash into the ocean, and we have several recent examples to draw from, generates substantial debris, the logical conclusion from the planting hypothesis is that the plane did not terminate in the ocean. I don't see how you can have it any other way.
- If the plane did not crash in the ocean, then the Inmarsat data must be incorrect or spoofed. The physics is very clear on this point. If the Inmarsat data is correct, the plane had to have been tracking in a Southerly direction at 19:40 at a minimum ground speed of 400 knots. The only landing place that could accommodate a 777 in that direction is located in the Cocos, and there is no evidence to suggest the plane landed in the Cocos.
- If the debris were planted, there has to be some strong motive for doing so. No one associated with the official search has indicated they believe that 9M-MRO terminated anywhere but in the SIO - not the Aussies, not the Malays, not the Chinese, and not any of their subcontractors or advisors. Planting debris is not needed to reinforce the notion of an SIO terminus, and doing so entails unnecessary and substantial risk of discovery. The only possible reason for advocating that the debris has been planted is to enable scenarios in which 9M-MRO did not terminate in the ocean.
- The recovered debris passes the "sniff" test. Experts who have had the opportunity to examine the debris have not publicly expressed any concern about its origin or authenticity. If the debris parts were removed from 9M-MRO or some other aircraft, subjected to damage, and placed in the ocean, detailed examination would raise a lot of flags. Crash forensics are highly refined, and it is unlikely that planted parts would go unnoticed.
Taken in aggregate the points above are difficult for a reasonable person to dismiss, particularly in the absence of any evidence to support the hypothesis that debris has been planted.
Saturday, December 10, 2016
Biofouling ??
Anecdotal pictures from my beach house.
Near Bowling Ball Beach - about half a mile North of my place. Purpose of picture was to capture gnarly piece in the middle of the photo which was a lot "cooler" than it appears in the photo.
Private beach (no name) directly below house at low tide.
Gualala Point Beach (near town about 4 miles South)
The reality is that stuff gets picked pretty clean shortly after it hits the beach. The North Coast Cali beaches are relatively pristine - no man made debris to speak of.
In answer to a person's question about what happens to biofouling. Ami walking on Gualala Point Beach. Gulls are voracious feeders, and they are well equipped to do so.
Why it is called Bowling Ball Beach (at low tide), in case anyone was wondering. A unique confluence of geology and the forces of nature.
For Johan, Swedish people do not screw around when building a cairn. Ami, adding the last touches beneath a glacier near Juneau, Alaska.
Near Bowling Ball Beach - about half a mile North of my place. Purpose of picture was to capture gnarly piece in the middle of the photo which was a lot "cooler" than it appears in the photo.
Private beach (no name) directly below house at low tide.
Gualala Point Beach (near town about 4 miles South)
The reality is that stuff gets picked pretty clean shortly after it hits the beach. The North Coast Cali beaches are relatively pristine - no man made debris to speak of.
In answer to a person's question about what happens to biofouling. Ami walking on Gualala Point Beach. Gulls are voracious feeders, and they are well equipped to do so.
Why it is called Bowling Ball Beach (at low tide), in case anyone was wondering. A unique confluence of geology and the forces of nature.
For Johan, Swedish people do not screw around when building a cairn. Ami, adding the last touches beneath a glacier near Juneau, Alaska.
Friday, December 9, 2016
JW Blog Stats - 2016
Just for shits and grins.
Number of Jeff-o-grams: 54
Mean posts per Jeff-o-gram: 348
Median posts per Jeff-o-gram: 334
Number of Jeff-o-grams: 54
Mean posts per Jeff-o-gram: 348
Median posts per Jeff-o-gram: 334
Subscribe to:
Comments (Atom)