ranking-and-race-data
The race is quite interesting in its own right. Fewer people have participated in it over the years than have climbed Mount Everest. It truly is daunting.
It also serves as an interesting test bed for statistical prediction.
Using the daily progress to date and a Monte Carlo simulation (500 trials). The winning time is predicted to be in the range of 65 to 69 days (95% probability). Previous record time was the last time the race was held in 2013, and was 78 days. The predicted improvement is largely attributed to boats with foils being used for the first time.
Another interesting statistical question is how many sailors will still be in the race when the winner arrives in France. This value was estimated using Poisson statistics, and is shown below. When the analysis below was run there were 10 abandons(8 declared officially and 2 more likely but undeclared). So the number of abandons at the end of the race (when winner crosses the line) should be in the range of 12 to 17 with high confidence, and with a predicted most likely value of 14/15. Since 29 boats started the race, that would imply 15/14 boats still heading to France.
The motive for posting this information is similar to the IG motive for sticking pins in a map. It serves the purpose of going on record with your analytics so they can be tested against reality in the future.
So, we shall see.
Update 23 December:
So, as the leader rounds Cape Horn it becomes obvious that the weather pattern heading North in the Atlantic is far different than the weather pattern that prevailed in the traverse from Good Hope to Cape Horn. As a consequence, the Monte Carlo simulation is likely to be too optimistic relative to predicting the finishing time. Hey, you can only do so much. The abandon model is not affected.
Update 24 December:
Leader's daily progress from start. Linear fit has been excellent, but it is unlikely to continue sailing North in the Atlantic.
Histogram of daily distance (48 days total) recorded by the leader. I have no explanation for the obvious bimodal distribution.
Update 27 December
So, I have a conjecture for the bimodal distribution above. The conjecture being that there is a threshold speed for the foil boats that produces two normal speed distributions - one above and one below the speed where the foils add lift. Of course, this will need to be checked by downloading the data for a non-foil boat such as Rich Wilson's. Just FYI the transition speed (if there is one) based on the bimodal distribution above is around 14.5 knots.
Update 28 December
So, I harvested the Rich Wilson data and plotted it on the same histogram using the same range bins as the above data plot.
The Wilson data does not exhibit the marked bimodal characteristic of the leading foil boat. I am not prepared to draw a broad conclusion here. Obviously more work needs to be done using data from other boats.
Update 2 January
Harvested the daily distance cover by Elies (non-foil boat) and plotted histogram (below).
There is not a hint of a bimodal distribution. This result tells me there is a threshold effect going on with the foil boats i.e. slower below a certain threshold, and a non-linear increase in speed above a certain threshold. Probably this non-linearity is to be expected? Foils create more drag below threshold, and provide a lift (step function reduction in drag) above a certain threshold. As stated above this threshold speed is in the neighborhood of 14.5 knots.
Update 3 January
The weather in the South Pacific has been horrible. Despite that Wilson put in an impressive 24hr run.
South Atlantic continues to slow the pace of the lead boats as the trend line below clearly shows.
Updated Wilson/Leader histogram. Wilson's data has regressed to essentially Gaussian form.
Winning time propagator has advanced to 69 days. My guess is that this advance will continue or perhaps even accelerate as the leaders hit the doldrums. MOQ is definitely closing in, and may well become a factor.
Update 4 January
Continuing to look at the daily distance distribution, I harvested the daily totals of CoQ, another foil boat, and plotted the histogram below.
Leader histogram reproduced again below for comparison.
CoQ does not exhibit a strong bimodal distribution. This data would seem to contradict the notion that there is a threshold effect with respect to the foil boats. While CoQ has achieved a higher daily distance than the leader, it is interesting to note that the number of days in which 450nm or more was achieved is 12 for the leader versus 4 for CoQ.
Update 6 January
So, being someone who sings the US National Anthem, I was curious to see what Monte Carlo had to say about Rich Wilson's finishing (Rich has better than a 66% chance of finishing). Histogram below.
Of course, weather is a huge factor as we are seeing relative to the obvious slow down in the lead boat relative to the trend line established earlier in the race.
Update 7 January
So, the French have thrown their hat into the ETA prediction ring. The linked article below appeared in the last day.
Of course, the later the prediction, the more information you have. There is also less uncertainty since there is less time remaining. While I stand my original estimate made some three weeks ago, if I were to update the Monte Carlo run with the following priors the result would be as shown below.
1> Leader was rounding Cape Horn on December 23 (day 48)
2> Leader currently has ~3000nm remaining distance to travel
3> Draw Monte Carlo samples from post Cape Horn data set (days 48-62)
The result above is in good agreement with the recent French prediction.
Update 10 January
For Rich Wilson followers a prediction below for when he is likely to round Cape Horn. All 500 Monte Carlo trials fell into bin days 71,72, and 73 with day 72 dominant with a ~70% probability.
update 12 January
So earlier I used Poisson statistics to compute how many boats would abandon by the time the lead boat finished. The question was posed in this way for my convenience. A much more difficult, and interesting, question to answer is how many boats will finish the race. To answer this question requires Weibull statistics which are much more difficult and tedious than Poisson (which is why I do not generally pose questions in that way).
The array below is the ordered percentage complete of the boats that have abandoned the race so far.
data = np.array([4,16,29,29,30,36,45,49,54,55,56]) #11 boats have officially abandoned the race
Additionally there are 18 boats still in the race. The array data above must be "censored". Censoring is a term mathematicians use for the need to adjust the failure rank by the number of "units" that have not failed at the time the calculation was performed.
When the array data (properly censored) is plotted on the standard Weibull ln-ln plot the result is as shown below. The extent to which these points fall on a straight line on a ln-ln plot is a measure of the appropriateness of the Weibull statistic.
Using linear regression a best fit straight line is fitted to the above data as shown below.
While not perfect, the straight line fit is far from horrible. The Weibull statistic should work pretty well. Extracting the slope and intercept of the linear regression yields the "shape" and "scale" factors of the Weibull distribution which allows the Weibull CDF (cumulative distribution function) to be plotted below.
The CDF shows that at 100% complete the percent abandoning is very close to 50%. So Weibull statistics predict that half the starting field (~15 boats) should be able to finish.
P.S. Earlier I mentioned that Wilson had better than a 66% chance of finishing. I got that number in a simplistic fashion. While true, the reality is that Wilson has a better than 80% chance of finishing now that a proper number for the total finishers has been computed.
(1) references from the weibull.nl website and also from this example of doing Weibull analysis using Excel.
(2) reference code from pybokeh at wakari.io Weibull Analysis Notebook
Update 14 January
Should have done this above, but neglected to do so (old and lazy). Check Weibull fit against the 11 failures to date. The failures to date are plotted as red dots in the Weibull CDF. As can be seen, the actual failures are running ahead of the Weibull prediction. However, there has not been a failure for some time now, so the actual data should revert to the Weibull prediction CDF as more boats fail.
While here I am here I may as well post the latest first boat ETA Monte Carlo. Used finer granularity and 10,000 trials. The French prediction of January 19 is day 74. The French prediction is looking pretty good right now, although it could easily spill over into January 20. Of course, I am sticking with the original Monte Carlo prediction of 73 days for statistical critique purposes. Perhaps we will have a "regression to the mean", and I will be able to pontificate on that.
Also below is the leader current daily distance. Obviously had the daily distance kept pace with the trend between Good Hope and The Horn there would have been partying going on in France a day or so ago.
Update 17 January
The first data point for statistical confirmation is "in the books". Rich Wilson rounded Cape Horn on January 16 at ~0300UTC which, according to my math, is race elapsed time of 71.63 hours. From Vendee website below:

The Monte Carlo prediction for the rounding is reproduced below.
More data on boat speed (histograms for 71 days) is shown below for Banque and CoQ, currently running 1st and 3rd respectively. The data is clearly not Gaussian, but shows evidence of "binning" with a bin separation near 10 knots and 15 knots. My speculation is the 10 knot null is due to a "hull speed" effect. The hull speed of a 60' boat is ~10 knots, 1.34*SQRT(60) ~ 10. The bin separation near 15 knots is due to the foils which are said to become effective around that speed.
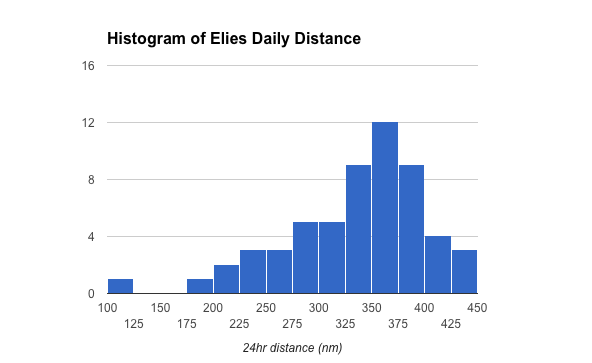
The tri-modality for CoQ is not as pronounced as Banque, but it is clearly there. The non-foil boats exhibit a histogram which is more nearly Gaussian, although there is a hint of a hull effect in the Elies data, a non foil boat, also shown below.
Update 19 January
The winning boat arrived in port today with an elapsed time of 74:03:36 , 74.15 days. This value is shown in red below on the Monte Carlo histogram derived earlier.
I am quite satisfied with this result, and will have more to say about the method and my impressions in a later post. For the moment it is safe to say that three factors (all weather related) place fundamental constraints on what accuracy might be achieved:
1> Distance traveled each day which, as I understand it, is the great circle distance covered in a 24 hour period. What is really of interest is the distance "made good".
2> A related issue is the total distance traveled. My simulation used a value of 25,260 nm whereas at the end of the race the leader had traveled 27,445 nm.
Without further study I am not prepared to say whether the above two effects act counter to each other or reinforce each other. My suspicion is the former since the accuracy turned out very well.
3> The weather itself is not predictable, and its effect is not equivalent to white noise that averages out.